Loonie and Aussie Share Downward Bond
In yesterday’s post (Tide is Turning for the Aussie), I explained how a prevailing sense of uncertainty in the markets has manifested itself in the form of a declining Australian Dollar. With today’s post, I’d like to carry that argument forward to the Canadian Dollar.
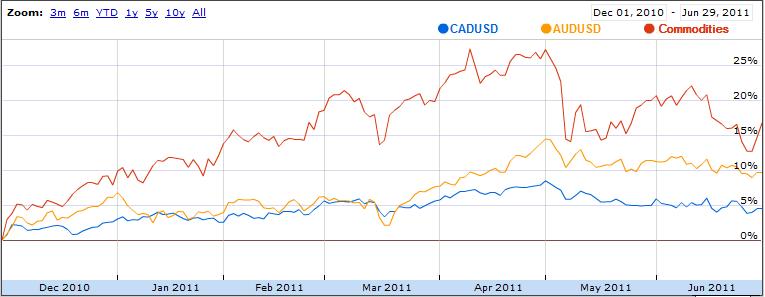
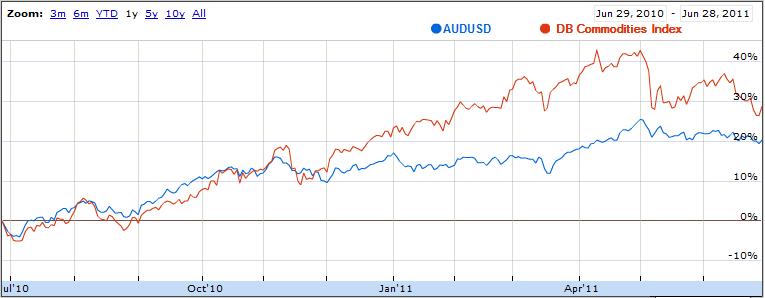
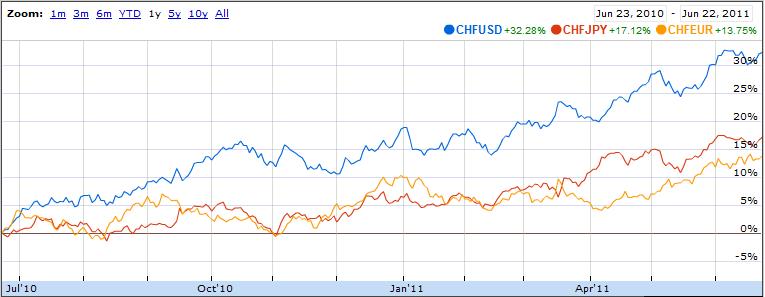
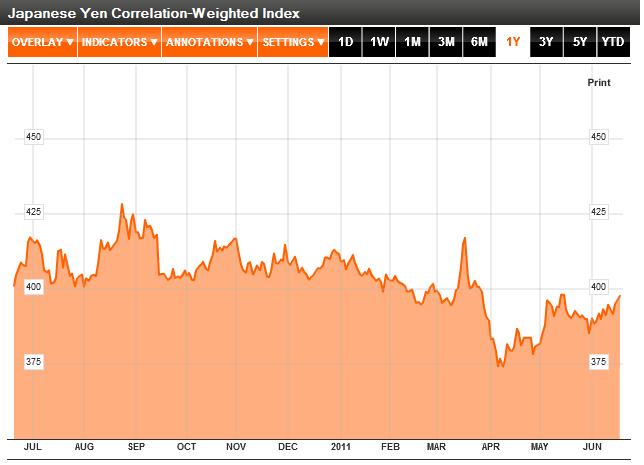
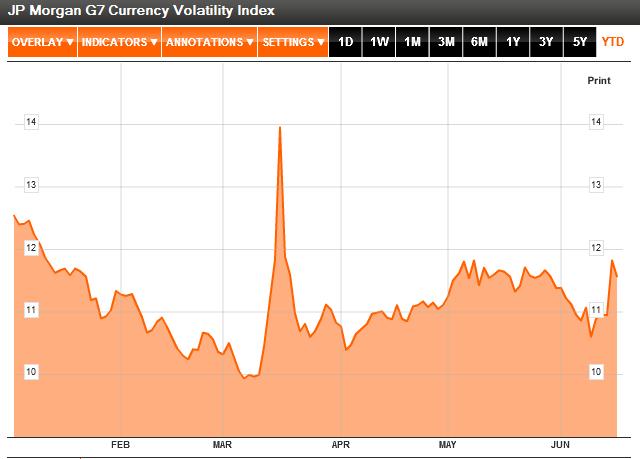
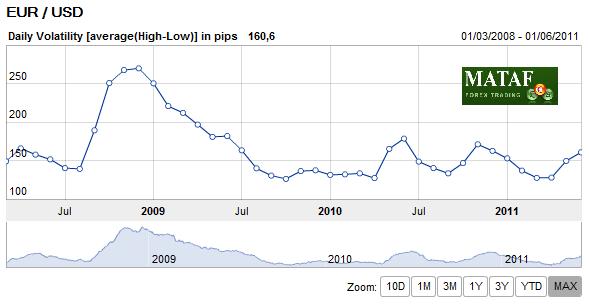
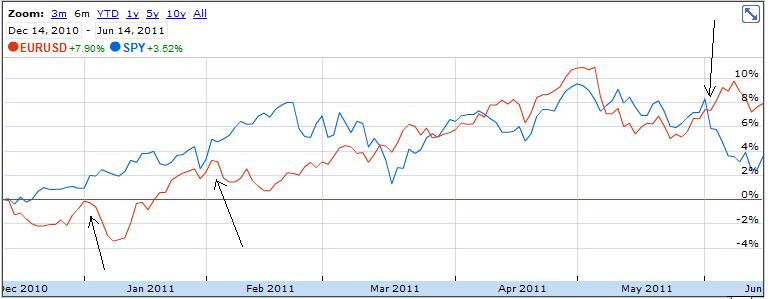
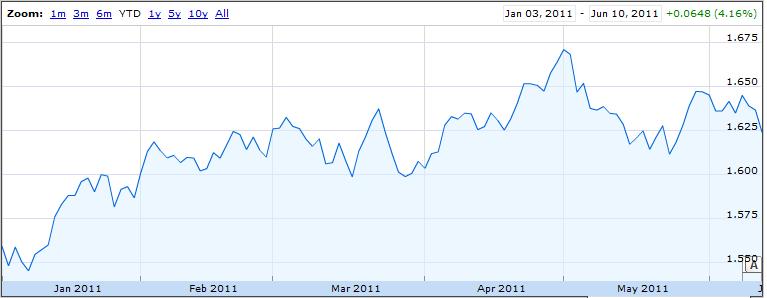
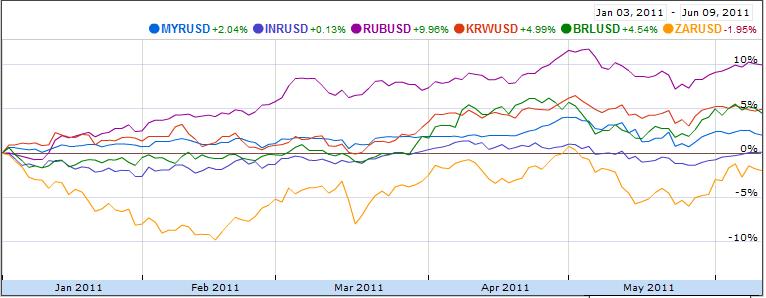
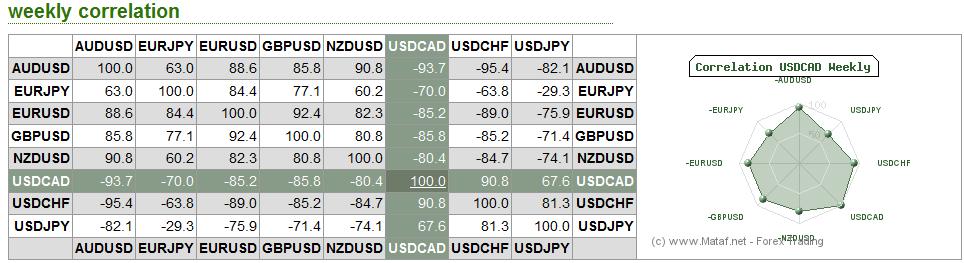
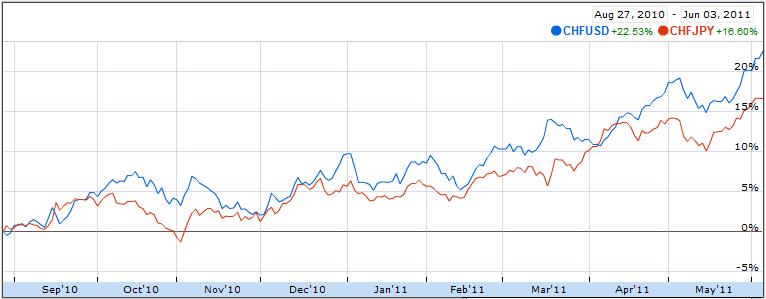
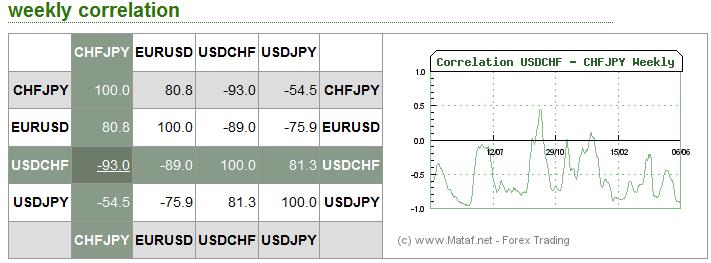
As it turns out, the forex markets are currently treating the Loonie and the Aussie as inseparable. According to Mataf.net, the AUD/USD and CAD/USD are trading with a 92.5% correlation, the second highest in forex (behind only the CHFUSD and AUDUSD). The fact that the two have been numerically correlated (see chart below) for the better part of 2011 can also be discerned with a cursory glance at the charts above.
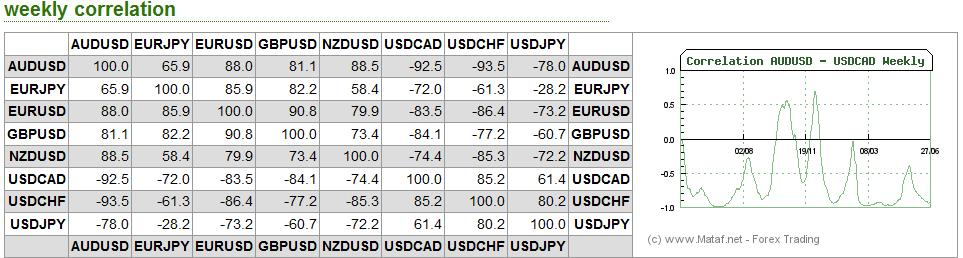
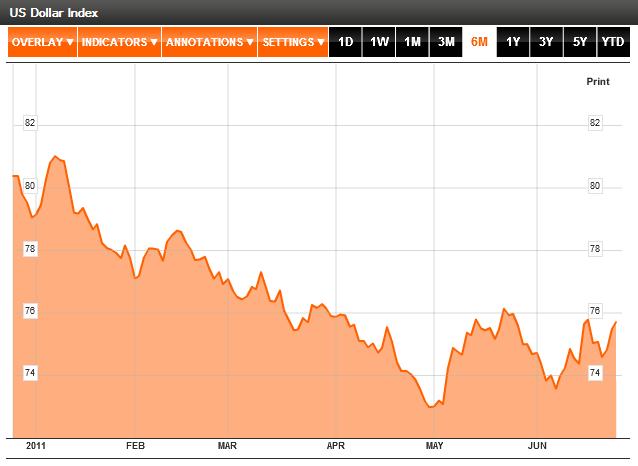
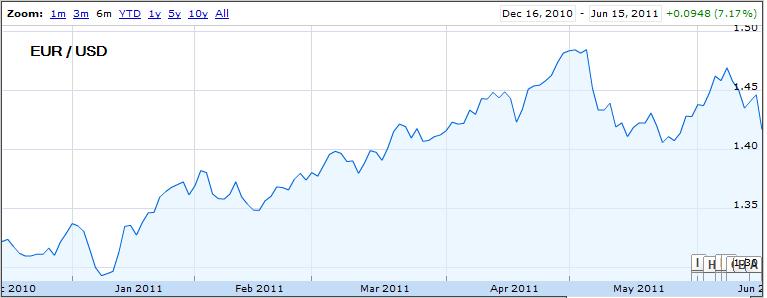
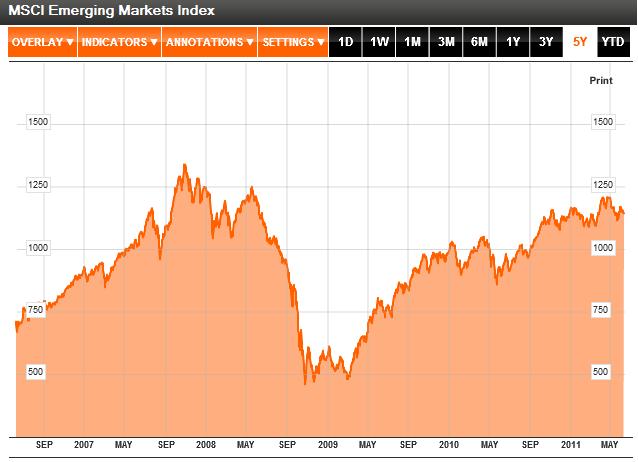
Why is this the case? As it turns out, there are a handful of reasons. First of all, both have earned the dubious characterization of “commodity currency,” which basically means that a rise in commodity prices is matched by a proportionate appreciation in the Aussie and Loonie, relative to the US dollar. You can see from the chart above that the year-long commodities boom and sudden drop corresponded with similar movement in commodity currencies. Likewise, yesterday’s rally coincided with the biggest one-day rise in the Canadian Dollar in the year-to-date.
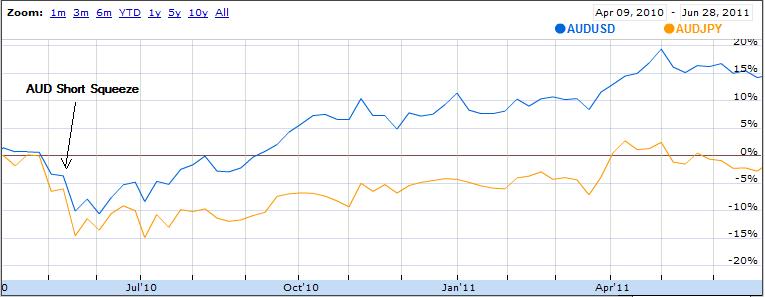
Beyond this, both currencies are seen as attractive proxies for risk. Even though the chaos in the eurozone has very little actual connection to the Loonie and Aussie (which are fiscally sound, geographically distinct, and economically insulated from the crisis), the two currencies have recently taken their cues from political developments in Greece, of all things. Given the heightened sensitivity to risk that has arisen both from the sovereign debt crisis and global economic slowdown, it’s no surprise that investors have responded cautiously by unwinding bets on the Canadian dollar.
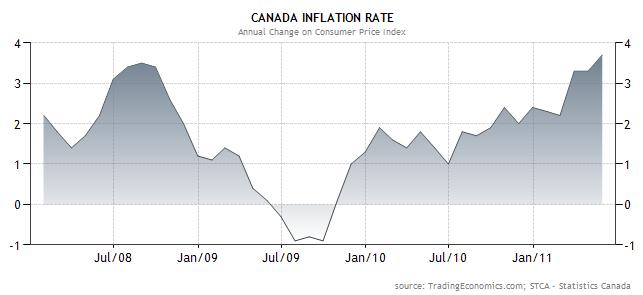
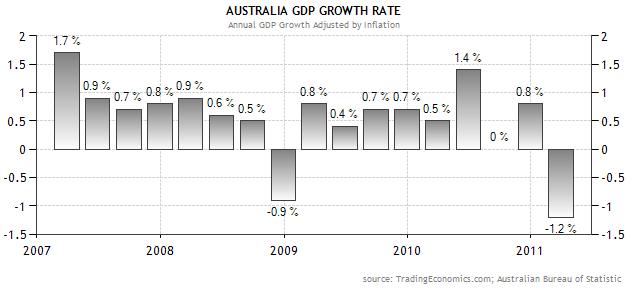
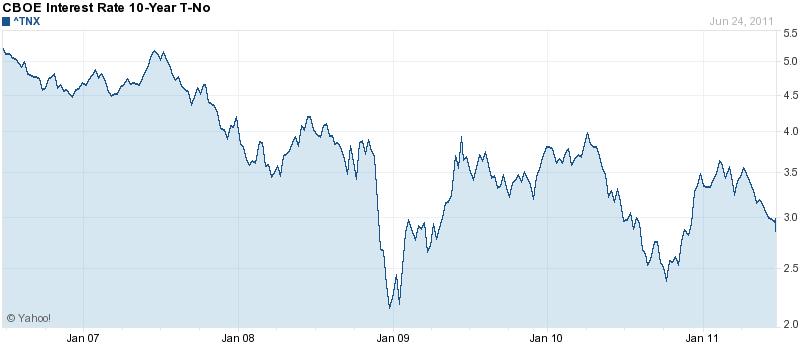
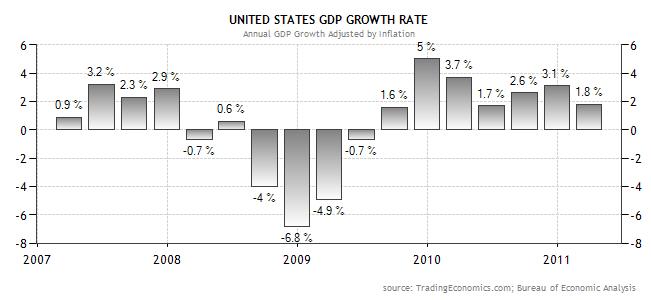
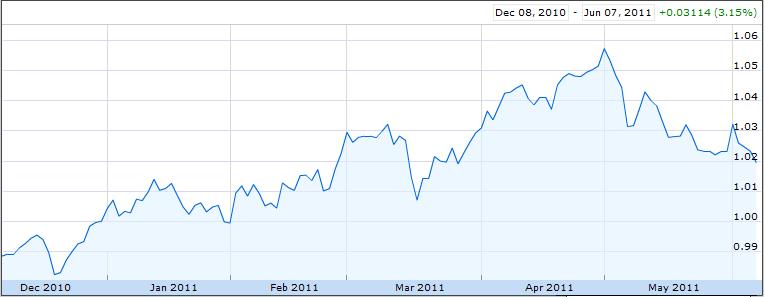
Finally, the Bank of Canada is in a very similar position to the Reserve Bank of Australia (RBA). Both central banks embarked on a cycle of monetary tightening in 2010, only to suspend rate hikes in 2011, due to uncertainty over near-term growth prospects. While GDP growth has indeed moderated in both countries, price inflation has not. In fact, the most recent reading of Canadian CPI was 3.7%, which is well above the BOC’s comfort zone. Further complicating the picture is the fact that the Loonie is near a record high, and the BOC remains wary of further stoking the fires of appreciation by making it more attractive to carry traders.
In the near-term, then, the prospects for further appreciation are not good. The currency’s rise was so solid in 2009-2010 that it now seems the forex markets may have gotten ahead of themselves. A pullback towards parity – and beyond – seems like the only realistic possibility. If/when the global economy stabilizes, central banks resume heightening, and risk appetite increases, you can be sure that the Loonie (and the Aussie) will pick up where they left off.